
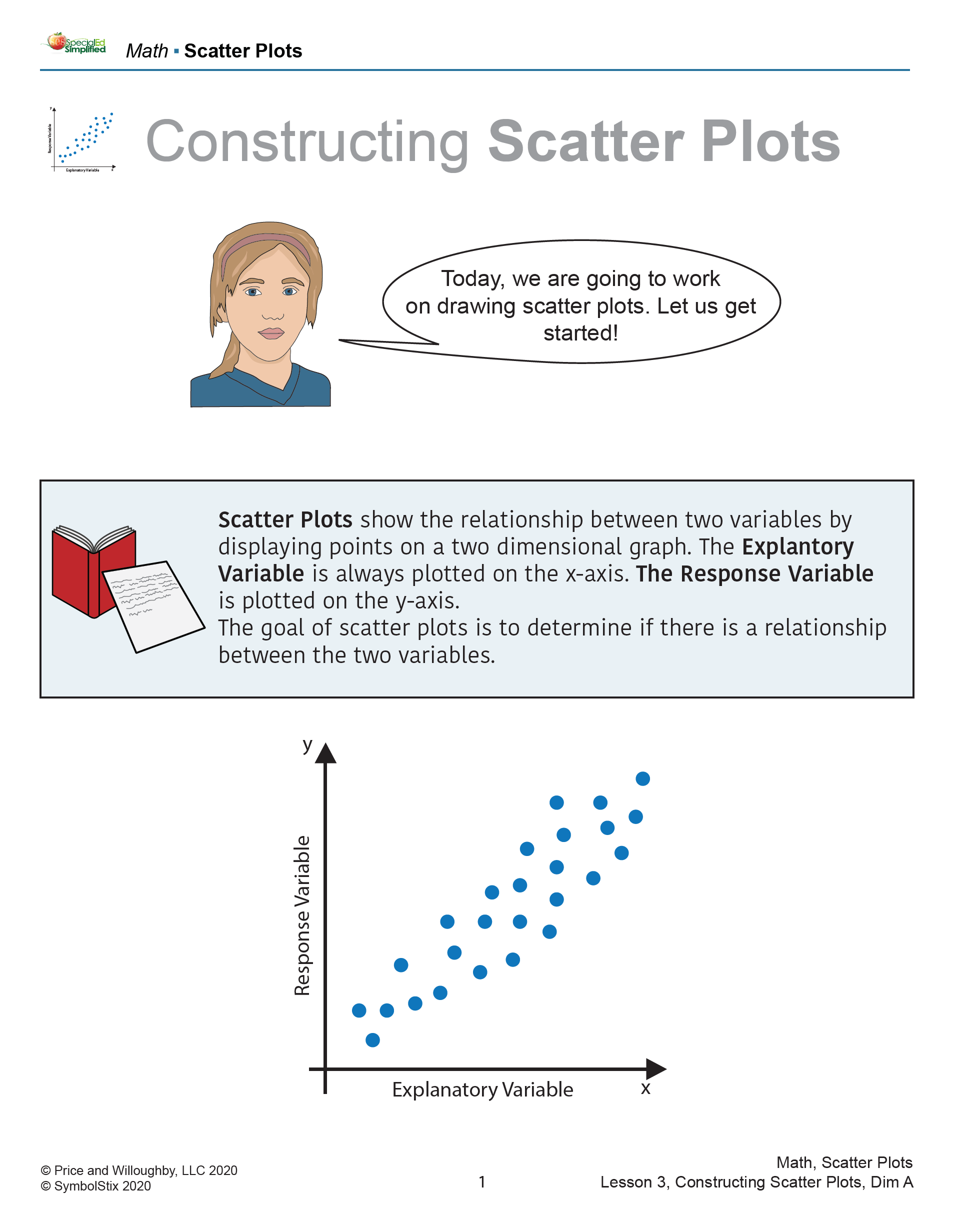
In a linear model we can use correlation to quantify the strength. Strength is about how close the dots are to the fitted line. Is the relationship positive or negative? For example, “as the distance a car has travelled increases, the asking price tends to decrease.” The term “tends to” is very useful here. It means a general tendency.Īssociation is about the direction. I would use the word “ shape” in preference. I don’t really like the use of the word “trend” here, as to me it should be used for time-series data only.
Trend covers the idea of whether the graph is linear or non-linear. The following uses the framework provided by R. Materials produced for teacher development, available on Census School suggest the following things to comment on: Trend, Association, Strength, Groups and unusual observations. Unfortunately the art of describing scatterplots is not as developed as music, and at times the terms are unclear and even used in different ways by different people. Just as musicians need to label different types of scales in order to communicate with each other their musical ideas, there is a specific vocabulary for describing graphs. Students also need examples of the different aspects that you would comment on in a graph, using appropriate vocabulary. The asking price of used Toyota sedans against the year of manufacture. The following graph has a strangely ordered look to it because the x-axis variable takes only whole numbers, and the prices are nearly always close to the nearest thousand. The reality of data is that quite often the nature of measurement and rounding means that the graph appears quite different from the classic scatter-plot. It helps to have some examples that aren’t beautifully behaved. Practice without feedback and correction can lead to entrenched mistakes.īecause graph interpretation is about pattern recognition, we need to have patterns that students can try to match the new graphs to. This is actually quite tricky for teachers to arrange, as you need to have lots of sets of data for students to look at, and you need to make sure they are giving correct answers. So how do we teach this? I think about how I learned to interpret graphs, and the answer is practice, practice, practice. Students should not be drawing graphs by hand. Students need to be exposed to a large number of different scatterplots, Fortunately this is now possible, thanks to computers. In a set of data about fast food, there appears to be a relationship between sodium content and energy. In the graph below, is there really a linear relationship, or is it just because of the choice of sample? However, if the sample of food taken is predominantly fast food, high sodium content is related to high fat content (salt on fries!) and this can appear to be a relationship. For example, a scatterplot of the sodium content vs the energy content in food should not really have a strong relationship. The nature of the individual observations, and the sample can make a big difference to the meaning drawn from the graph. There is also a contextual content to the discussion. A few unusual observations can affect how we see the graph. My experience is that people tend to try for more complicated models than is sensible. What one person sees as a non-linear relationship, another person might see as a line with some unusual observations. In addition, there is considerable room for argument in interpreting scatterplots. This can be likened to a master chess player who can look at a game in play and see at a glance what is happening, whereas the novice sees only the individual pieces, and cannot easily tell where the action is taking place. The problem is that when you know what to look for, spurious effects don’t get in the way, but when you don’t know what to look for, you don’t know what is spurious. On a scatterplot we can see what shape the data seems to have, what direction the relationship goes in, how close the points are to the line, if there are clear groups and if there are unusual observations. When undertaking an investigation of bivariate measurement data, a scatterplot is the graph to use. This post is about the challenges of teaching scatterplot interpretation, with some suggestions. Graph interpretation is a difficult skill to teach as there is no clear algorithm, such as mathematics teachers are used to teaching, and the answers are far from clear-cut. Patterns, vocab and practice, practice, practiceĪn important part of statistical analysis is being able to look at graphical representation of data, extract meaning and make comments about it, particularly related to the context.


 0 kommentar(er)
0 kommentar(er)
